Chapter10 - Boolean Logic
3.01 Logic Gates
Key Terms
- Logic gate - the basic foundation of a digital circuit that controls the flow of electronic signals.
- Digital circuit - a circuit where electronic signals are one of two values, high voltage (l) or low voltage (0).
- Voltage - the potential difference across an electrical component needed to make electricity flow through it.
- Microprocessor - an integrated circuit that provides the same functions of a CPU.
- Truth table - a way of showing every outcome of a logic gate.
Logic Gates
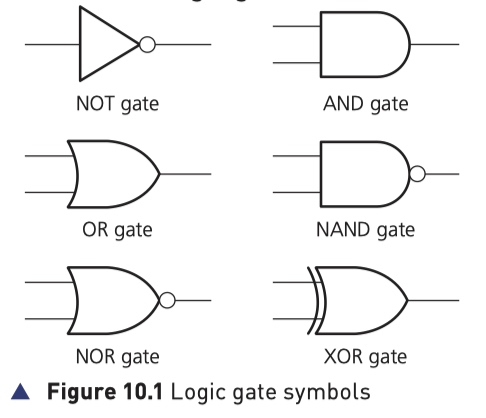
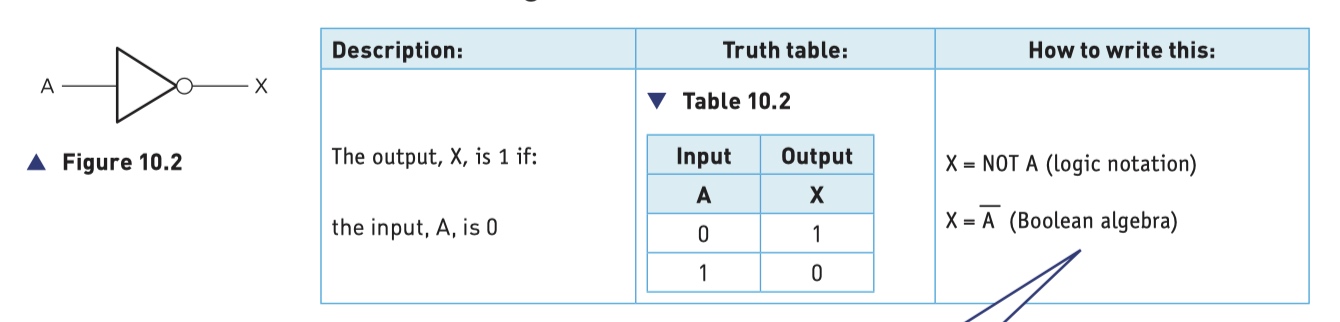
NOT Gate
AND Gate
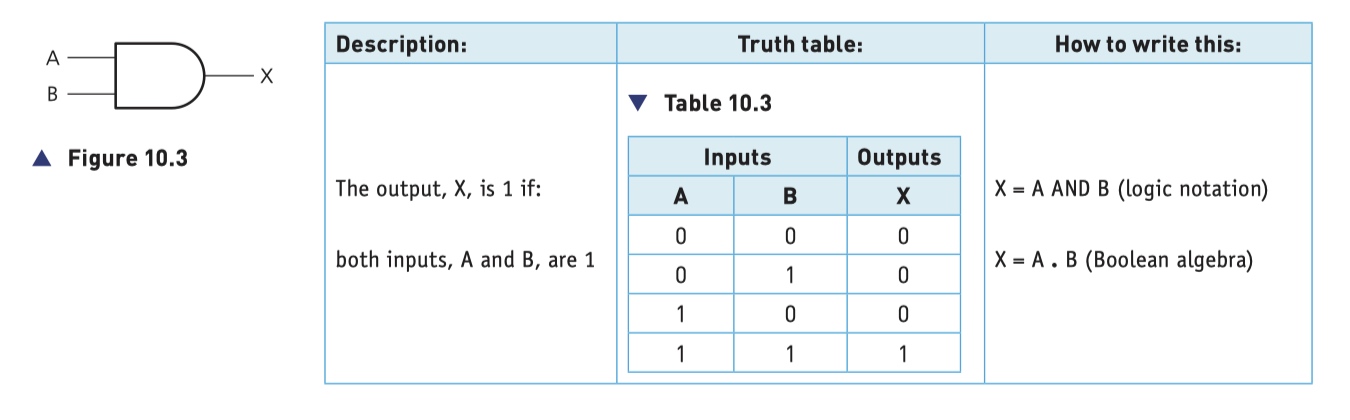
OR Gate
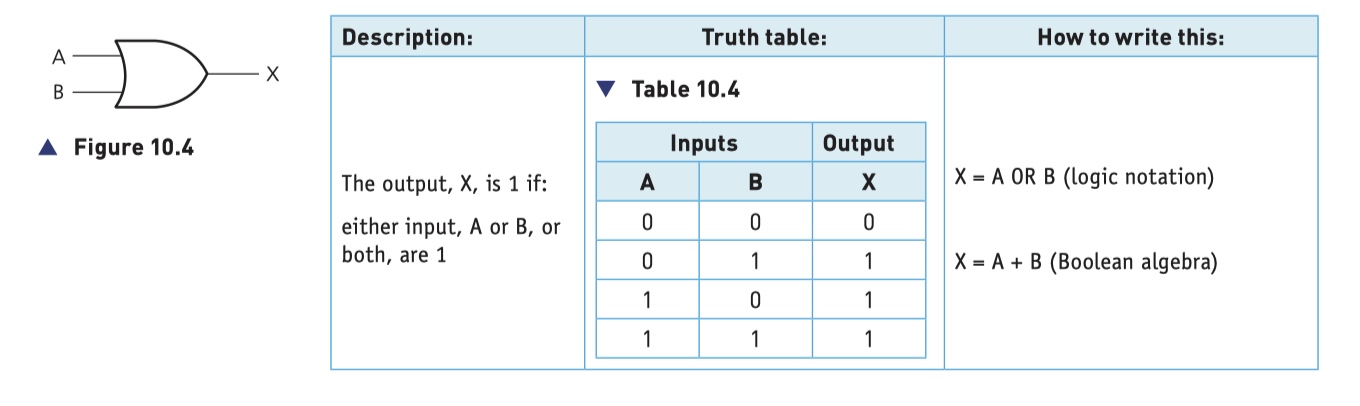
NAND Gate (NOT AND)
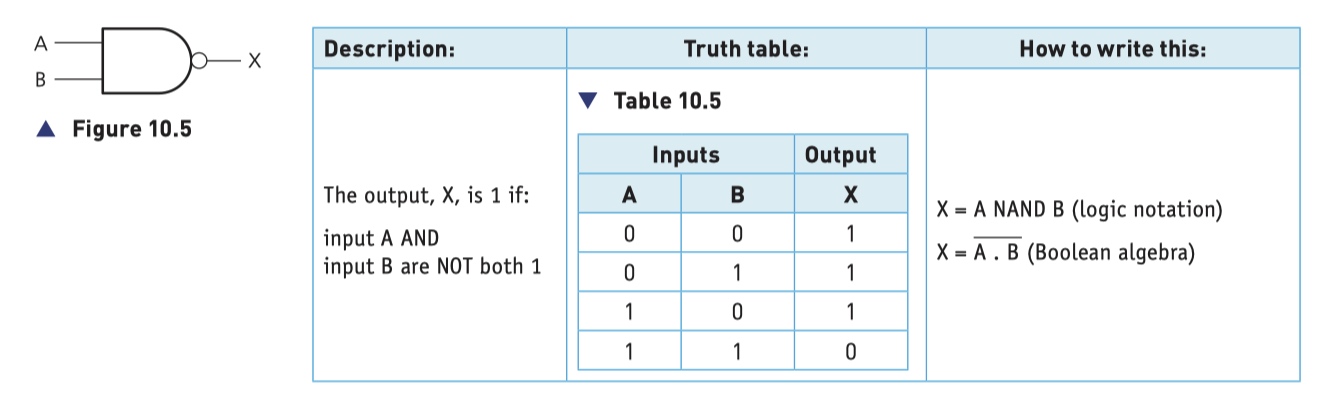
NOR Gate (NOT OR)
XOR Gate (XOR Gate)
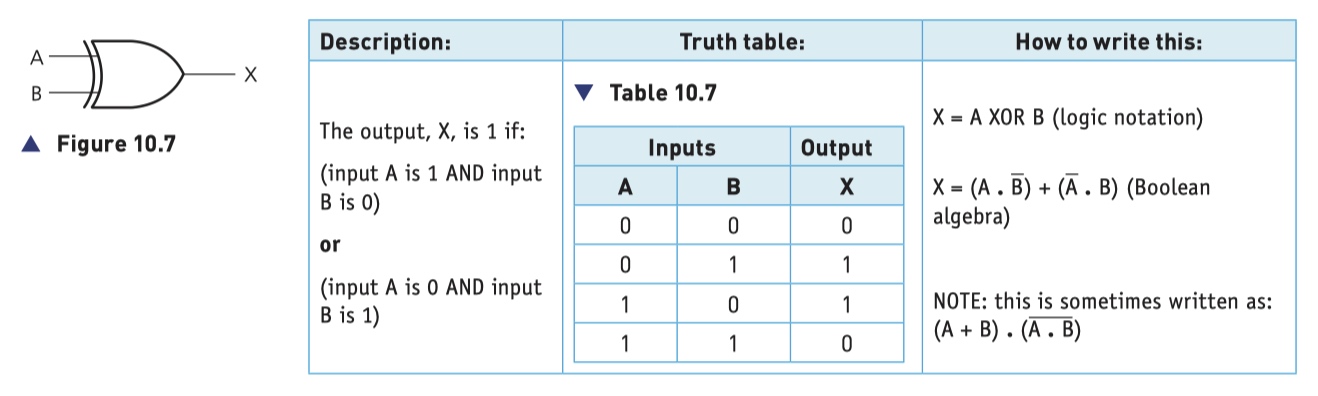
- . represents the AND operation
- + represents the OR operation
- a bar (above the letter or letters, e.g. a) represents the NOT operation.
Logic circuits, logic expressions, truth tables and problem statements
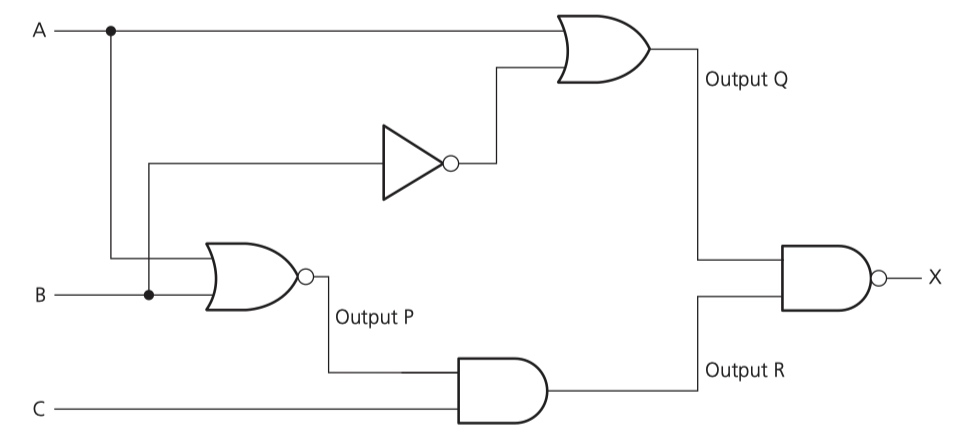
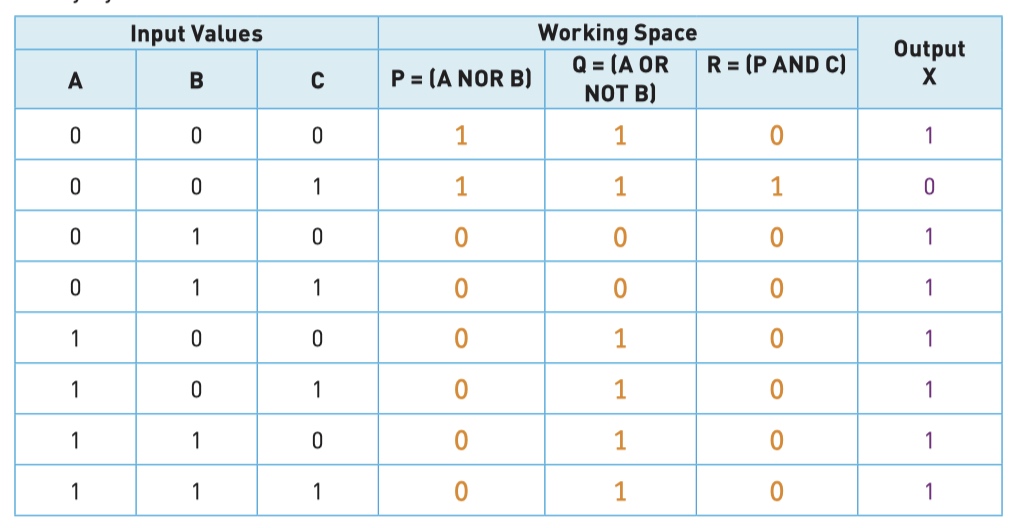
Type 1 - produce a truth table for a given logic circuit
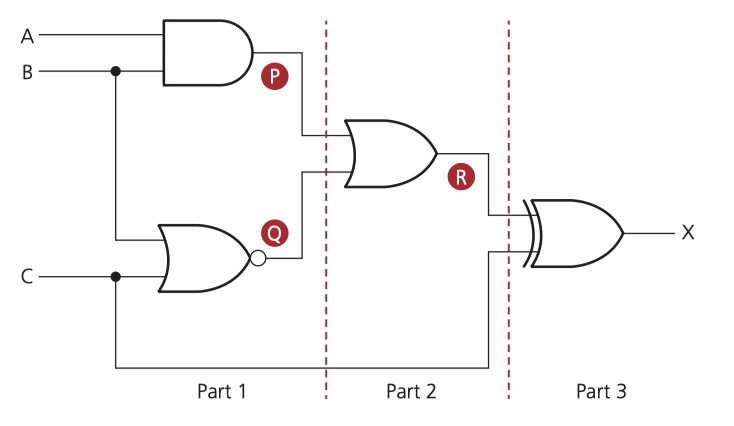
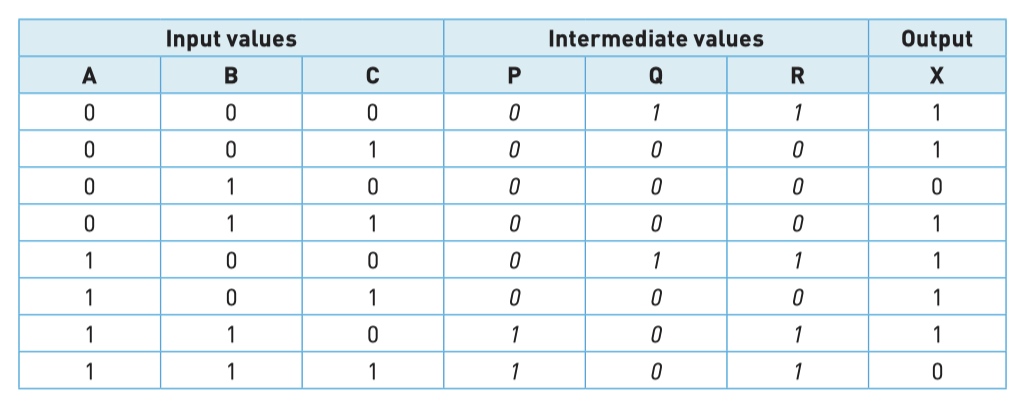
题目:找出对应逻辑图(logic circuit)的真值表(truth table)
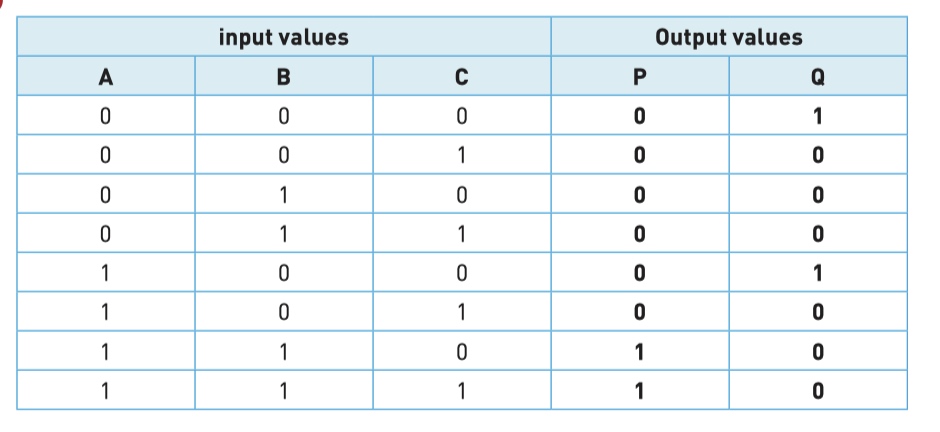
Step 1 - find the intermediate values P and Q

找出对应逻辑图(logic circuit)的真值表(truth table)
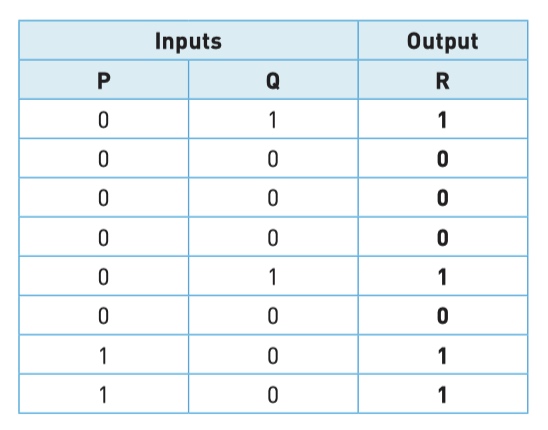
Step 2 - find intermediate values R use P and Q

找出对应逻辑图(logic circuit)的真值表(truth table)
Step 3 - find final part X use intermediate R and C

找出对应逻辑图(logic circuit)的真值表(truth table)
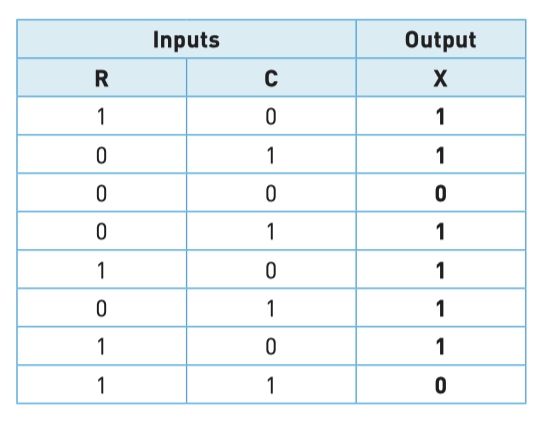
Final result

找出对应逻辑图(logic circuit)的真值表(truth table)
Type 2 - write logic expressions from given logic circuits
Example 1
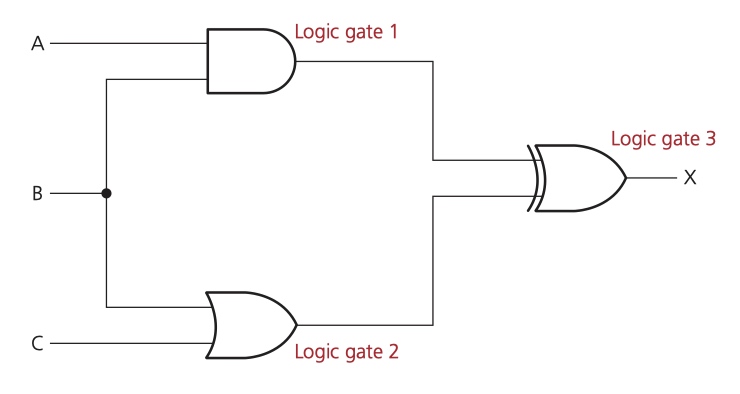
- logic gate1::
(A AND B) - logic gate2::
(B OR C) - final result::
(A AND B) XOR (B OR C)
Example 2
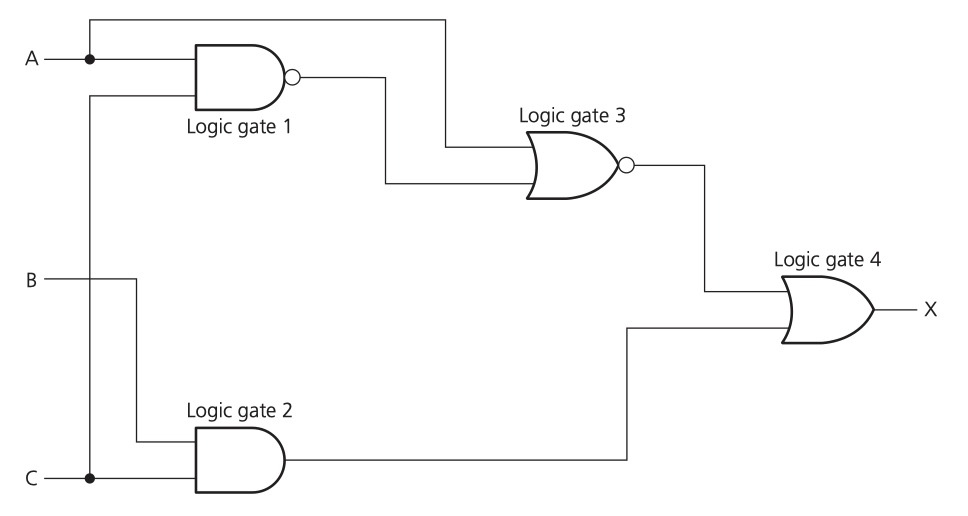
- logic gate 1::
(A NAND C) - logic gate 2::
(B AND C) - logic gate 3::
(logic gate 1) NOR A ~ ((A NAND C) NOR A) - logic gate 4::
((A NAND C) NOR A) OR (B AND C)
Type 3 - produce a logic circuit and a truth table from given logic expression
Example 1
Given logic expression: (A XOR C) OR (NOT C NAND B)
first step - A XOR C
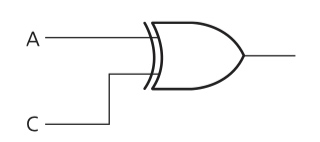
second step - NOT C NAND B
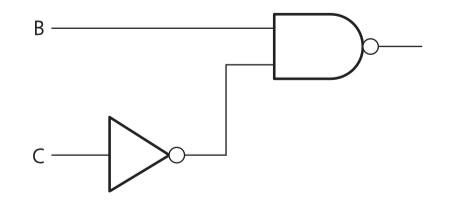
third step - combine
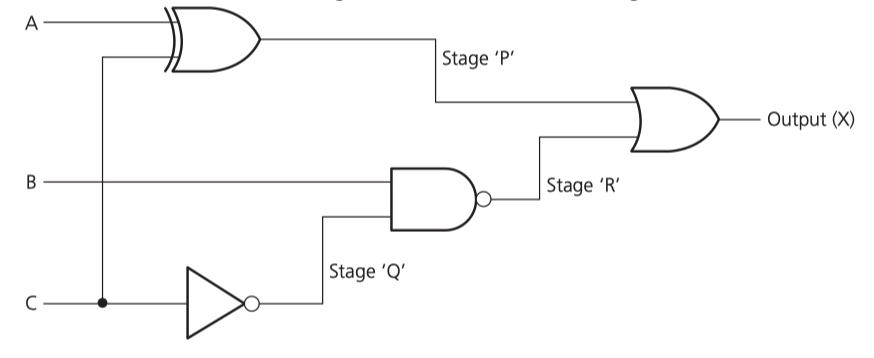
fourth step - truth table
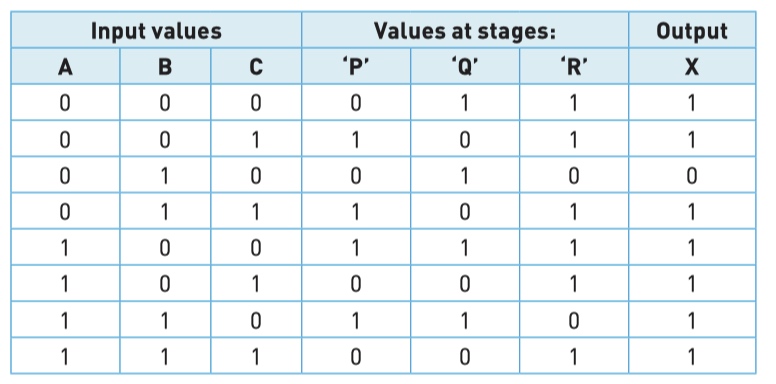
Type 4 - produce a logic expression and logic circuit from given truth table (optional)
Example 1
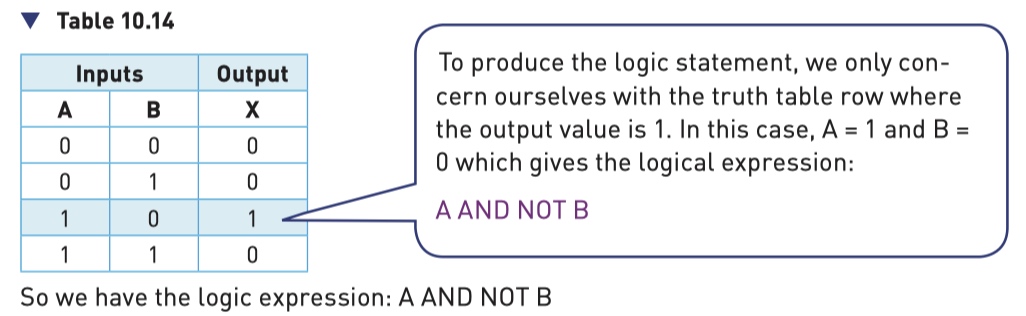
logic circuit
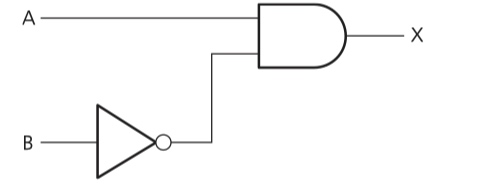
Example 2

logic circuit
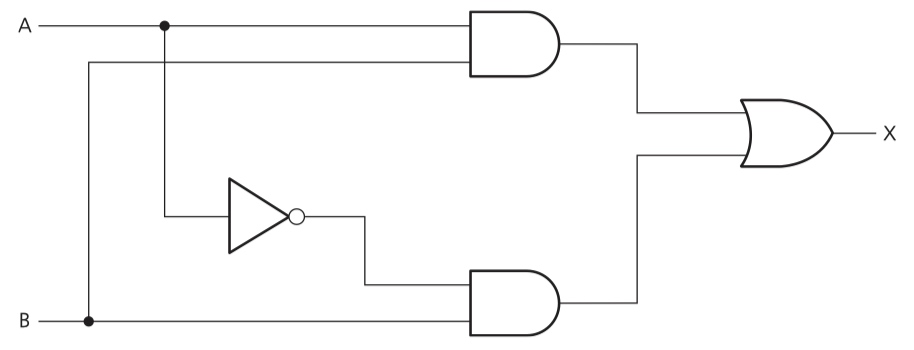
Example 3
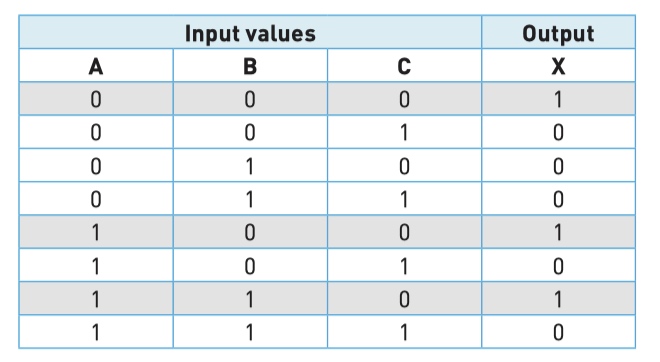
(NOT A AND NOT B AND NOT C)
(A AND NOT B AND NOT C)
(A AND B AND NOT C)
final logic expression
(NOT A AND NOT B AND NOT C)
OR (A AND NOT B AND NOT C)
OR (A AND B AND NOT C)
Type 4 - Produce a logic circuit and truth table from real work case
example 1
A safety system uses three inputs to a logic circuit. An alarm, X, sounds if input A represents ON and input B represents OFF; or if input B represents ON and input C represents OFF.
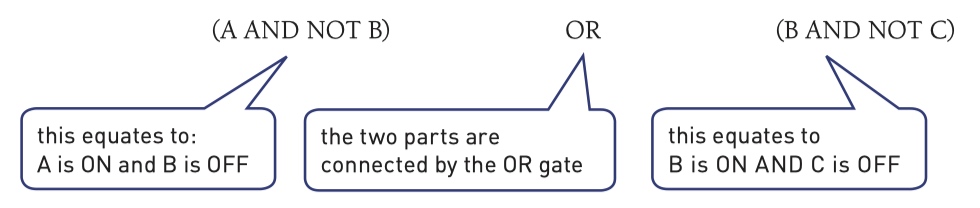
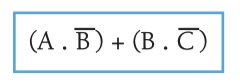
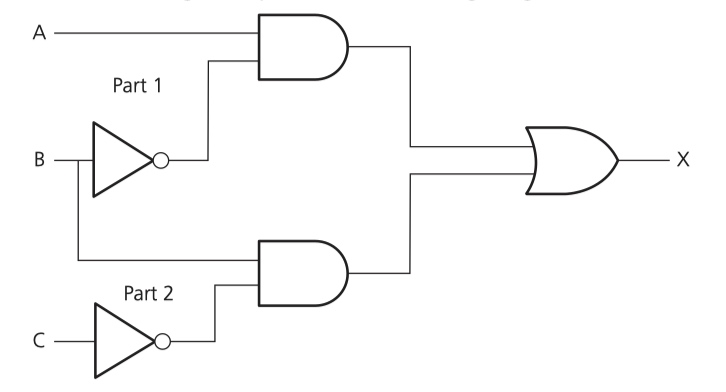
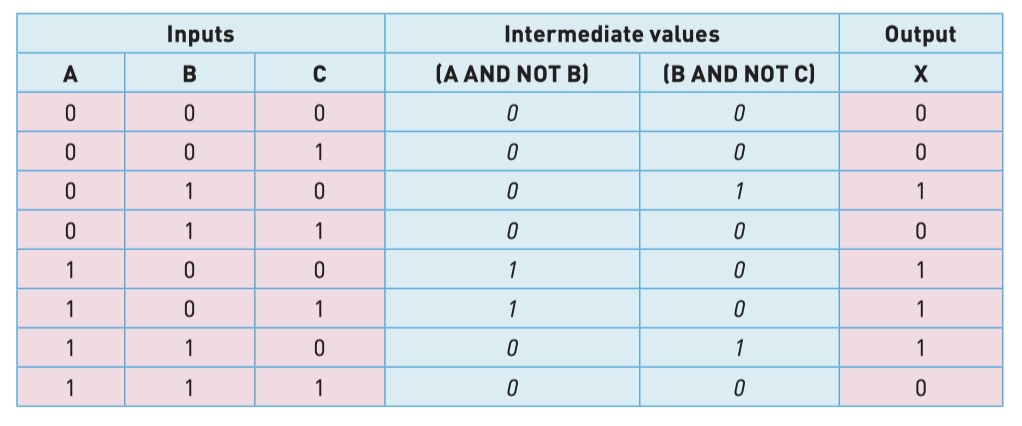
Type 5 Produce the working space (optional)
example 1
Consider the logic statement:
((A NOR B) AND C) NAND (A OR NOT B)
- Draw a logic circuit to represent the given logic statement.
- Complete the truth table for the given logic statement.
- P = (A NOR B)
- Q = (A OR NOT B)
- R = (P AND C)