ALevel-CS Chapter 13
Data types and structures
13.01 Data types
Promitive data types
Primitive data types(atomic data types) are those variables that can be defined simply by commands built into the programming language.
- Integer - whole number
- REAL - a number with a decimal point
- TRUE or FALSE - Conditions
- BOOLEAN - logical values
- CHAR - single character
Further data types
string - store serveral characters
The string data type is known as a structured type because it is essentially a sequence of characters.
Pseudocode data types
| INTEGER | A signed while number |
|---|---|
| READ | A signed number with a decimal point |
| CHAR | A single character |
| STRING | A sequence of zero or more characters |
| BOOLEAN | The logical value TRUE and FALSE |
| DATE | A date consisting of day, month and year, sometimes including a time in hours, minutes and seconds |
13.02 The record type
Record type
Sometimes variables of different data types are a logical group, such as data about a person (name, date of birth, height, number of siblings, whether they are a full-time student).
Name is a STRING; date of birth is a DATE; height is a REAL; number of siblings is an INTEGER; whether they are a full-time student is a BOOLEAN.
We can declare a record type to suit our purposes. The record type is known as a user-defined type, because the programmer can decide which variables (fields) to include as a record.
Pseudocode
// declare a record type
TYPE <TypeIdentifier>
DECLARE <field identifier> : <data type>
.
.
ENDTYPE
// declare a variable of this recode type
DECLARE <variable identifier> : <record type>
// access an individual filed using the dot notation
<variable identifier>.<field identifier>
Pseudocode Example
// declare a Persion record type
TYPE PersonType
Name : STRING
DateOfBirth : DATE
Height : REAL
NumberOfSiblings : INTEGER
IsFullTimeStudent : BOOLEAN
ENDTYPE
// declare a variable of this type
DECLARE Person : PersonType
// assign a value to a file of this Person record
Person.Name ← "Fred"
Person.NumberOfSiblings ← 3
Person.IsFullTimeStudent ← TRUE
// output a field
OUTPUT Person.Name
13.03 Arrays
Key Terms
- Array index - row or column number of an individual array element
- Upper bound - the highest number index of an array dimension
- Lower bound - the smallest number index of an array dimension
Arrays
An array is an ordered set of data items, usually of the same type, grouped together using a single identifier.
Individual array elements are addressed using an array index for each array dimension.
- list - one-dimensional (1D) array
- table(matrix) - two-dimensional (2D) array
When writting pseudocode, arrays need to be declared before they are uses.
13.04 One-dimensional arrays
Key Terms
- Linear search - checking each element of an array in turn for a required value
- Bubble sort - a sort method where adjacent pairs of values are compared and swapped
One-dimensional array
// 1D array declaration
DECLARE <arrayIdentifier> : ARRAY[<lowerBound>:<upperBound>] OF <dataType>
// pseudocode example
DECLARE List1 : ARRAY[1:3] OF STRING // 3 elements in this list
DECLARE List2 : ARRAY[0:5] OF INTEGER // 6 elements in this list
DECLARE List3 : ARRAY[1:100] OF INTEGER // 100 elements in this list
DECLARE List4 : ARRAY[0:25] OF CHAR // 26 elements in this list
// accessing 1D array
<arrayIdentifier>[x]
// pseudocode example
NList[25] ← 0
AList[3] ← 'D'
Example 1 - Working with one-dimensional array
Requirement
Take seven numbers as input and store them for later use.
Pseudocode
FOR Index ← 0 TO 6
INPUT MyList[Index]
NEXT Index
Linear Search - Searching a 1D array
Requirement
Take a number as input. Search for this number in an existing 1D array of seven numbers
Identifier

Pseudocode
MaxIndex ← 6
INPUT SearchValue
Found ← FALSE
Index ← –1
REPEAT
Index ← Index + 1
IF MyList[Index] = SearchValue
THEN
Found ← TRUE
ENDIF
UNTIL FOUND = TRUE OR Index >= MaxIndex
IF Found = TRUE
THEN
OUTPUT "Value found at location: " Index
ELSE
OUTPUT "Value not found"
ENDIF
Bubble sort - sorting element in 1D array



Identifier table
simplest way
- Compare the first and second values. If the first value is larger than the second value, swap them.
- Compare the second and third values. If the second value is larger than the third value, swap them.
- Compare the third and fourth values. If the third value is larger than the fourth value, swap them.
- Keep on comparing adjacent values, swapping them if necessary, until the last two values in the list have been processed.
Pseudocode
n ← MaxIndex – 1
FOR i ← 0 TO MaxIndex – 1
FOR j ← 0 TO n
IF MyList[j] > MyList[j + 1]
THEN
Temp ← MyList[j]
MyList[j] ← MyList[j + 1]
MyList[j + 1] ← Temp
ENDIF
NEXT j
n ← n – 1 // this means the next time round the inner loop, we don't
// look at the values already in the correct positions.
NEXT i
improved bubble sort algorithm
improved
We can use a variable NoMoreSwaps to store whether or not a swap has taken place during the current pass. We initialise the variable NoMoreSwaps to TRUE. When we swap a pair of values we set NoMoreSwaps to FALSE. At the end of the pass through the array we can check whether a swap has taken place.
identifier table

Pseudocode
n ← MaxIndex – 1
REPEAT
NoMoreSwaps ← TRUE
FOR j ← 0 TO n
IF MyList[j] > MyList[j + 1]
THEN
Temp ← MyList[j]
MyList[j] ← MyList[j + 1]
MyList[j + 1] ← Temp
NoMoreSwaps ← FALSE
ENDIF
NEXT j
n ← n – 1
UNTIL NoMoreSwaps = TRUE
13.05 Two-dimensional arrays
Two-dimensional arrays
// declaration
DECLARE <identifier> : ARRAY[<lBound1>:<uBound1>, <lBound2>:<uBound2>] OF <dataType>
# example
Board : ARRAY[1:6,1:7] OF INTEGER
// Accessing 2D arrays
<arrayIdentifier>[x,y]
# example
Board[3,4] ← 0 // sets the element in row 3 and column 4 to zero
Example - Working with two-dimensional arrays and nested loops
// set each element of array to zero
FOR Row ← 0 TO MaxRowIndex
FOR Column ← 0 TO MaxColumnIndex
ThisTable[Row, Column] ← 0
NEXT Column
NEXT Row
// output
FOR Row ← 0 TO MaxRowIndex
FOR Column ← 0 TO MaxColumnIndex
OUTPUT ThisTable[Row, Column] // stay on same line
NEXT Column
OUTPUT Newline // move to next line for next row
NEXT Row
13.06 Text files
Text files
Data need to be stored permanently. One approach is to use a file.
A text file consists of a sequence of characters formatted into lines. Each line is terminated by an end-of-line marker. The text file is terminated by an end-of-file marker.
Text file pseudocode
// writing a text file
OPENFILE <filename> FOR WRITE //open the file for writing
WRITEFILE <filename>, <stringValue> //write a line of text to the file
CLOSEFILE <filename> //close file
// reading from a text file
OPENFILE <filename> FOR READ // open file for reading
READFILE <filename>, <stringVariable> // read a line of text from the file
CLOSEFILE <filename> // close file
// Appending to a text file
OPENFILE <filename> FOR APPEND // open file for append
WRITEFILE <filename>, <stringValue> // write a line of text to the file
CLOSEFILE <filename> // close file
// The end-of-file(EOF) marker
OPENFILE "Test.txt" FOR READ
WHILE NOT EOF("Test.txt") DO
READFILE "Test.txt", TextString
OUTPUT TextString
ENDWHILE
CLOSEFILE "Test.txt"
13.07 Abstract Data Types (ADTs)
Key Terms
- Abstract Data Type - a collection of data with associated operations
Abstract Data Types (ADTs)
An Abstract Data Type is a collection of data and a set of associated operations::
- create a new instance of the data structure
- find an element in the data structure
- insert a new element into the data structure
- delete an element from the data structure
- access all elements stored in the data structure in a systematic manner.
The remainder of this chapter describes the following ADTs:: stack, queue and linked list. It also demonstrates how they can be implemented from arrays.
13.08 Stacks
Stack
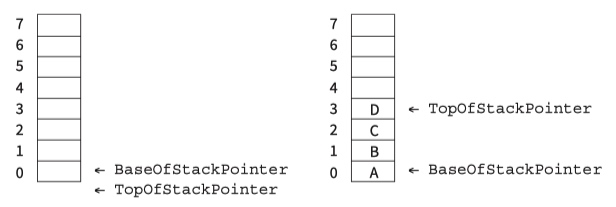
To make a stack, we pile items on top of each other. The item that is accessible is the one on top of the stack.
// implement stack using a 1D array
DECLARE Stack: ARRAY[0:7] OF CHAR
13.09 Queue
When people form a queue, they join the queue at the end. People leave the queue from the front of the queue.

a circular queue after 11 items have joined and five items have left the queue.

13.10 Linked lists
Key Terms
- Node - an element of a list
- Pointer - a variable that stores the address of the node it points to
- Null pointer - a pointer that does not point at anything
- Start pointer - a variable that stores the address of the first element of a linked list
Linked List
linear list - the list items are stored in consecutive locations.
An element of a list is called a node. A node can consist of several data items and a pointer, which is a variable that stores the address of the node it points to.
A pointer that does not point at anything is called a null pointer. It is usually represented by ∅. A variable that stores the address of the first element is called a start pointer.
