ALevel-CS Chapter 12

Algorithm design and problem-solving

12.01 What is computational thinking?

computational thinking

Computational thinking involves four key strands:: abstraction, decomposition, data modelling, pattern recognition and algorithmic thinking.

computational thinking

Abstraction

Abstraction gives us the power to deal with complexity.

An algorithm is an abstraction of a process that takes inputs, executes a sequence of steps, and produces outputs.

An abstract data type defines an abstract set of values and operations for manipulating those values.

Decomposition

Decomposition means breaking problems down into sub-problems in order to explain a process more clearly. Decomposition leads us to the concept of program modules and using procedures and functions.

Data modelling

Data modelling involves analysing and organising data. We can set up abstract data types to model real-world concepts, such as queues or stacks.

Pattern recognition

Pattern recognition means looking for patterns or common solutions to common problems and using these to complete tasks in a more efficient and effective way.

Algorithm design

Algorithm design involves developing step-by-step instructions to solve a problem.

12.02 What is an algorithm?

12.03 Expressing algorithm

Key Terms

Structured English:: a subset of the English language that consists of command statements used to describe an algorithm
Pseudocode:: a way of using keywords and identifiers to describe an algorithm without following the syntax of a particular programming language
Flowchart:: shapes linked together to represent the sequential steps of an algorithm

Expressing algorithm

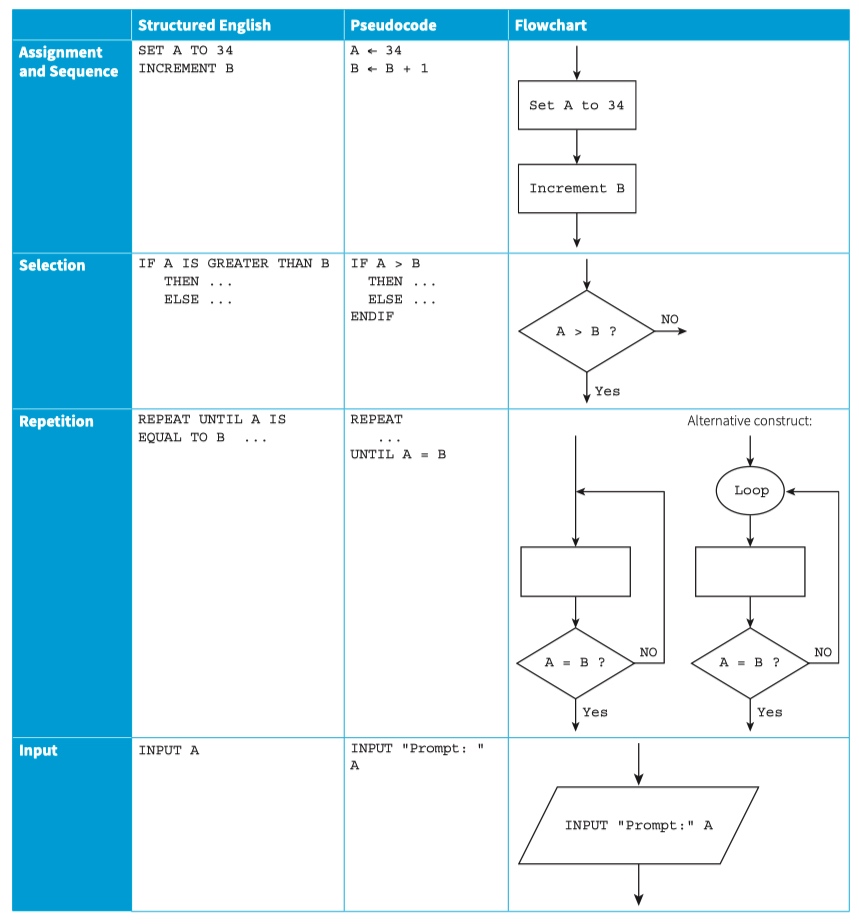
expression

Assignment: a value is given a name (identifier) or the value associated with a given identifier is changed.
Sequence: a number of steps are performed, one after the other.
Selection: under certain conditions some steps are performed, otherwise different (or no) steps are performed.
Repetition: a sequence of steps is performed a number of times. This is also known as iteration or looping.

12.04 Variables

Key Terms

Variable - a storage location for a data value that has an identifier

Variables

We need to be able to refer to a specific memory location so that we can write statements of what to do with the value stored there. We refer to these named memory locations as variables.

You can imagine these variables like boxes with name labels on them. When a value is input, it is stored in the box with the specified name (identifier) on it.

12.05 Assignments

Key Terms

Identifier table - a table listing the variable identifiers required for the solution, with explanations and data types.

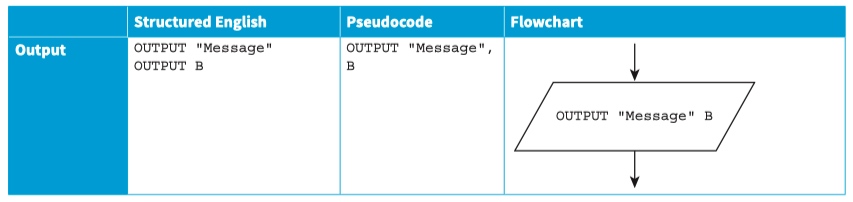
assigning value

Assigning a value

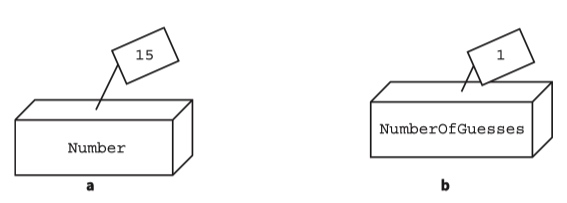
INPUT Number

NumberOfGuesses ← 1

Updating a value

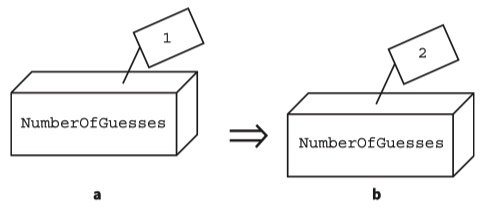
NumberOfGuesses ← NumberOfGuesses + 1

Copying a value

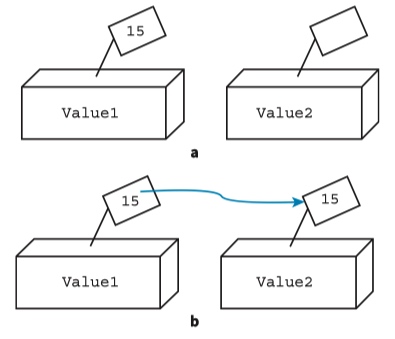
Value2 ← Value1

Swapping two values

Temp ← Value1 
Value1 ← Value2 
Value2 ← Temp

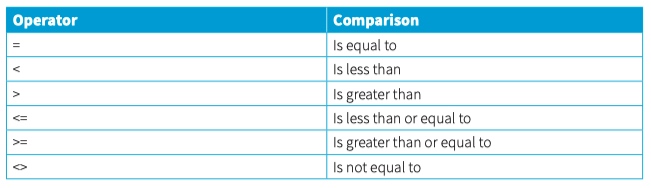
12.06 Logic statements

Key Terms

Nested IF statements - conditional statements within conditional statements

Logic statements

IF A < B 
    THEN 
        <statement(s)> 
    ELSE 
        <statement(s)> 
ENDIF

IF Guess = SecretNumber
    THEN 
        OUTPUT "Well done. You have guessed the secret number" 
    ELSE
        IF Guess > SecretNumber AND NumberofGuesses = 10
            THEN 
                OUTPUT "You still have not guessed the secret number" 
            ELSE 
                IF Guess > SecretNumber 
                    THEN 
                        OUTPUT "secret number is smaller" 
                    ELSE 
                        OUTPUT "secret number is greater" 
                ENDIF 
        ENDIF 
ENDIF

12.07 Loops

Key Terms

Rogue value - a value used to terminate a sequence of values Nested loop - loop containing another loop

Example 1 - Repetition using REPEAT UNTIL

Requirement

The problem to be solved:: Take 10 numbers as input and output the largest number.

Identifier

Pseudocode

INPUT BiggestSoFar 
Counter ← 1 
REPEAT 
    INPUT NextNumber 
    Counter ← Counter + 1 
    IF NextNumber > BiggestSoFar 
        THEN 
            BiggestSoFar ← NextNumber 
    ENDIF 
UNTIL Counter = 10 
OUTPUT BiggestSoFar

Example 2 - Repetition using FOR NEXT

Requirement

The problem to be solved:: Take 10 numbers as input and output the largest number.

Identifier

Pseudocode

INPUT BiggestSoFar 
FOR Counter ← 2 TO 10 
    INPUT NextNumber 
    IF NextNumber > BiggestSoFar 
        THEN 
            BiggestSoFar ← NextNumber 
    ENDIF 
NEXT Counter 
OUTPUT BiggestSoFar

Example 3 - Repetition using a rogue value

Requirement

A sequence of non-zero numbers is terminated by 0. Take this sequence as input and output the largest number.

Identifier

Pseudocode

INPUT BiggestSoFar 
REPEAT 
    INPUT NextNumber 
    IF NextNumber > BiggestSoFar 
        THEN 
            BiggestSoFar ← NextNumber 
    ENDIF 
UNTIL NextNumber = 0 
OUTPUT BiggestSoFar

INPUT NextNumber 
BiggestSoFar ← NextNumber 
WHILE NextNumber <> 0 DO // sequence terminator not encountered
    INPUT NextNumber
    IF NextNumber > BiggestSoFar
        THEN
            BiggestSoFar ← NextNumber
    ENDIF
ENDWHILE 
OUTPUT BiggestSoFar

Example 4 - Implementing the number-guessing game with a loop

requirement

The player repeatedly inputs a number to guess the secret number stored.
If the guess is correct, the number of guesses made is output and the game stops.
If the number input is larger than the secret number, the player is given the message to input a smaller number.
If the number input is smaller than the secret number, the player is given the message to input a larger number.

structured english

SET value for secret number 
REPEAT the following UNTIL correct guess 
    INPUT guess 
    count number of guesses 
    COMPARE guess with secret number 
    OUTPUT comment 
OUTPUT number of guesses

Identifier

flowchart

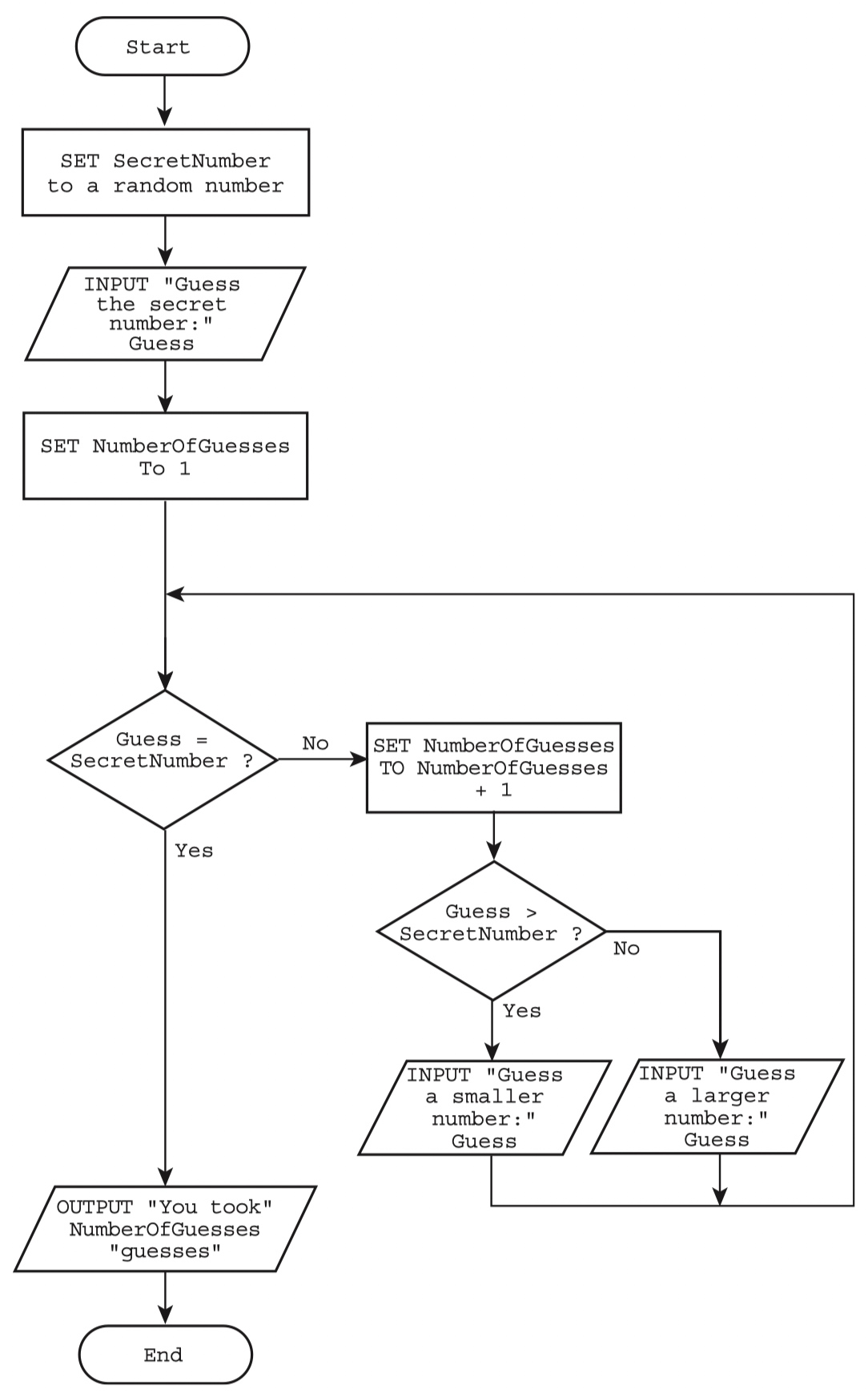
pseudocode - post-condition loop

SecretNumber ← Random 
NumberOfGuesses ← 0 
REPEAT
    INPUT Guess 
    NumberOfGuesses ← NumberOfGuesses + 1 
    IF Guess > SecretNumber
        THEN 
            // the player is given the message to input a smaller number 
    ENDIF 
    IF Guess < SecretNumber 
        THEN 
            // the player is given the message to input a larger number 
    ENDIF 
UNTIL Guess = SecretNumber 
OUTPUT NumberOfGuesses

pseudocode - pre-condition loop

SecretNumber ← Random 
INPUT Guess 
NumberOfGuesses ← 1 
WHILE Guess <> SecretNumber DO 
    IF Guess > SecretNumber 
        THEN 
            // the player is given the message to input a smaller number
    ENDIF 
    IF Guess < SecretNumber 
        THEN 
            // the player is given the message to input a larger number 
    ENDIF 
    INPUT Guess 
    NumberOfGuesses ← NumberOfGuesses + 1 
ENDWHILE 
OUTPUT NumberOfGuesses

Example 5 - Calculating running totals and averages

Requirement

Take 10 numbers as input and output the sum of these numbers and the average.

Identifier

Pseudocode

RunningTotal ← 0 
FOR Counter ← 1 TO 10
    INPUT NextNumber
    RunningTotal ← RunningTotal + NextNumber 
NEXT Counter 
OUTPUT RunningTotal 
Average ← RunningTotal / 10 
OUTPUT Average

Example 6 - Using nested loops

Requirement

Take as input two numbers and a symbol. Output a grid made up entirely of the chosen symbol, with the number of rows matching the first number input and the number of columns matching the second number input.

&&&&&&&

Identifier

Pseudocode - nested loop

INPUT NumberOfRows 
INPUT NumberOfColumns 
INPUT Symbol 
FOR RowCounter ← 1 TO NumberOfRows
    FOR ColumnCounter ← 1 TO NumberOfColumns
        OUTPUT Symbol // without moving to next line
    NEXT ColumnCounter
    OUTPUT Newline // move to the next line 
NEXT RowCounter

12.08 Stepwise refinement

Key Terms

Stepwise refinement - breaking down the steps of an outline solution into smaller and smaller steps

Example 1 - Drawing a pyramid using stepwise refinement

Requirement

Take as input a chosen symbol and an odd number. Output a pyramid shape made up entirely of the chosen symbol, with the number of symbols in the final row matching the number input.

    A
   AAA
  AAAAA
 AAAAAAA
AAAAAAAAA

structured english

Set up initial values 
REPEAT
    Output number of spaces
    Output number of symbols
    Adjust number of spaces and number of symbols to be output in next row UNTIL the required number of symbols have been output in one row

identifier

step 06 - check whether the number of sysbols for the next row is greater than the value input at the begining

UNTIL NumberOfSymbols > MaxNumberOfSymbols

Step

step 01 - Set up initial values expands into::

INPUT Symbol
INPUT MaxNumberOfSymbols
NumberOfSpaces ← (MaxNumberOfSymbols – 1) / 2
NumberOfSymbols ← 1

step 02 - Make sure the input is an odd number

REPEAT
    INPUT MaxNumberOfSymbols
UNTIL MaxNumberOfSymbols MOD 2 = 1
// MOD 2 gives the remainder after integer division by 2

step 03 - Output number of spaces enpands into

FOR i ← 1 TO NumberOfSpaces
    OUTPUT Space // without moving to next line
NEXT i

step 04 - Output number of symbols expands into::

FOR i ← 1 TO NumberOfSymbols
    OUTPUT Symbol // without moving to next line
NEXT i
OUTPUT Newline // move to the next line

step 05 - Adjust values for next row expends into

NumberOfSpaces ← NumberOfSpaces – 1
NumberOfSymbols ← NumberOfSymbols + 2

Pseudocode All

// Set Values
INPUT Symbol
// Input max number of symbols (an odd number)
REPEAT
    INPUT MaxNumberOfSymbols
UNTIL MaxNumberOfSymbols MOD 2 = 1
NumberOfSpaces ← (MaxNumberOfSymbols – 1) / 2
NumberOfSymbols ← 1 
REPEAT
    // Output number of spaces
    FOR i ← 1 TO 
        OUTPUT Space // without moving to next line
    NEXT i
    // Output number of symbols
    FOR i ← 1 TO NumberOfSymbols
        OUTPUT Symbol // without moving to next line
    NEXT i
    OUTPUT Newline // move to the next line
    // Adjust Values For Next Row
    NumberOfSpaces ← NumberOfSpaces – 1
    NumberOfSymbols ← NumberOfSymbols + 2
UNTIL NumberOfSymbols > MaxNumberOfSymbols

12.09 Modules

Key Terms

Procedure - a sequence of steps that is given an identifier and can be called to perform a sub-task
Function - a sequence of steps that is given an identifier and returns a single value; function call is part of an expression
Local variable - a variable that is accessible only within the module in which it is declared
Global variable - a variable that is accessible from all modules

Procedure

Example - CALL SetValues

CALL SetValues 
REPEAT
    CALL OutputSpaces
    CALL OutputSymbols
    CALL AdjustValuesForNextRow 
UNTIL NumberOfSymbols > MaxNumberOfSymbols

definitions

PROCEDURE SetValues 
    INPUT Symbol 
    CALL InputMaxNumberOfSymbols // need to ensure it is an odd number 
    NumberOfSpaces ← (MaxNumberOfSymbols - 1) / 2 
    NumberOfSymbols ← 1 
ENDPROCEDURE

PROCEDURE InputMaxNumberOfSymbols 
    REPEAT 
        INPUT MaxNumberOfSymbols 
    UNTIL MaxNumberOfSymbols MOD 2 = 1 
ENDPROCEDURE

PROCEDURE OutputSpaces 
    FOR Count1 ← 1 TO NumberOfSpaces 
        OUTPUT Space // without moving to next line 
    NEXT Count1 
ENDPROCEDURE

PROCEDURE OutputSymbols 
    FOR Count2 ← 1 TO NumberOfSymbols 
        OUTPUT Symbol // without moving to next line 
    NEXT Count2 
    OUTPUT Newline // move to the next line 
ENDPROCEDURE

PROCEDURE AdjustValuesForNextRow 
    NumberOfSpaces ← NumberOfSpaces – 1 
    NumberOfSymbols ← NumberOfSymbols + 2 
ENDPROCEDURE

function

Example

CALL SetValues 
REPEAT 
    CALL OutputSpaces 
    CALL OutputSymbols 
    NumberOfSpaces ← AdjustedNumberOfSpaces 
    NumberOfSymbols ← AdjustedNumbeOfSymbols 
UNTIL NumberOfSymbols > MaxNumberOfSymbols

PROCEDURE SetValues 
    INPUT Symbol 
    MaxNumberOfSymbols ← ValidatedMaxNumberOfSymbols 
    NumberOfSpaces ← (MaxNumberOfSymbols - 1) / 2 
    NumberOfSymbols ← 1 
ENDPROCEDURE

FUNCTION ValidatedMaxNumberOfSymbols RETURNS INTEGER 
    REPEAT 
        INPUT MaxNumberOfSymbols 
    UNTIL MaxNumberOfSymbols MOD 2 = 1 
    RETURN MaxNumberOfSymbols 
ENDFUNCTION

PROCEDURE OutputSpaces 
    FOR Count1 ← 1 TO NumberOfSpaces 
        OUTPUT Space // without moving to next line 
    NEXT Count1 
ENDPROCEDURE

PROCEDURE OutputSymbols 
    FOR Count2 ← 1 TO NumberOfSymbols 
        OUTPUT Symbol // without moving to next line 
    NEXT Count2 
    OUTPUT Newline // move to the next line 
ENDPROCEDURE

FUNCTION AdjustedNumberOfSpaces RETURNS INTEGER 
    NumberOfSpaces ← NumberOfSpaces – 1 
    RETURN NumberOfSpaces 
ENDFUNCTION

FUNCTION AdjustedNumberOfSymbols RETURNS INTEGER 
    NumberOfSymbols ← NumberOfSymbols + 2 
    RETURN NumberOfSymbols 
ENDFUNCTION