ALevel-CS Chapter 04
Logic gates and logic circuits
4.01 Boolean logic and problem statements
Key Terms
- Logic proposition - a statement that is either TRUE or FALSE
- Problem statement - an informal definition of an outcome which is dependent on one logic proposition or a combination of two or more logic propositions
Boolean logic and problem statements
Logic proposition can have only one of the two alternative Boolean logic values:: TRUE or FALSE.
4.02 Boolean operators
Key Terms
- Logic expression - logic propositions combined using Boolean operators, which may be equated to a defined outcome
Boolean operators
The three basic Boolean operators are AND, OR and NOT.
- A AND B is TRUE if A is TRUE and B is TRUE
- A OR B is TRUE if A is TRUE or B is TRUE
- NOT A is TRUE if A is FALSE.
- A NAND B is TRUE if A is FALSE or B is FALSE
- A NOR B is TRUE if A is FALSE and B is FALSE
- A XOR B is TRUE if A is TRUE or B is true but not both of them.
Truth tables

The truth table for the AND operator
4.04 Logic circuits and logic gates
Key Terms
- Logic gate - a component of a logic circuit that has an operation matching that of a Boolean operator
Logic circuits and logic gates

Example Constructing a logic circuit from a problem statement or logic expression
Consider the following problem statement:: A bank offers a special lending rate to customers subject to certain conditions. To qualify, a customer must satisfy certain criteria.
- The customer has been with the bank for two years.
- Two of the following conditions must also apply
- the customer is married
- the customer is aged 25 years or older
- the customer’s parents are customers of the bank.
To convert this statement to a logic expression using symbols we can choose:
- let A represent an account held for two years
- let B represent that the customer is married
- let C represent that the customer is aged 25 years or older
- let D represent that the customer’s parents have an account.
The logic expression can then be written as::
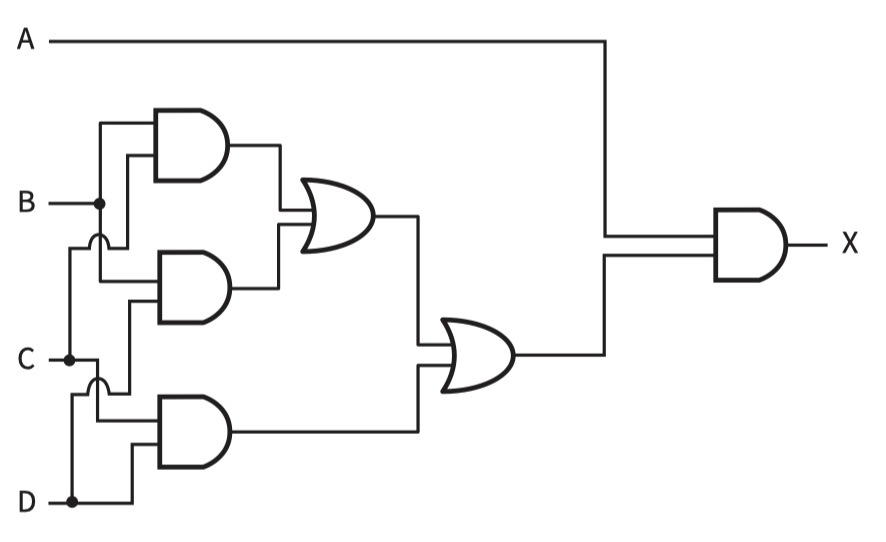
A AND (((B AND C) OR (B AND D)) OR (C AND D))
This could alternatively be presented with an outcome::
Special_rate IF A AND (((B AND C) OR (B AND D)) OR (C AND D))
alternatively as
X = A AND (((B AND C) OR (B AND D)) OR (C AND D))
NOT Gate

AND Gate

OR Gate

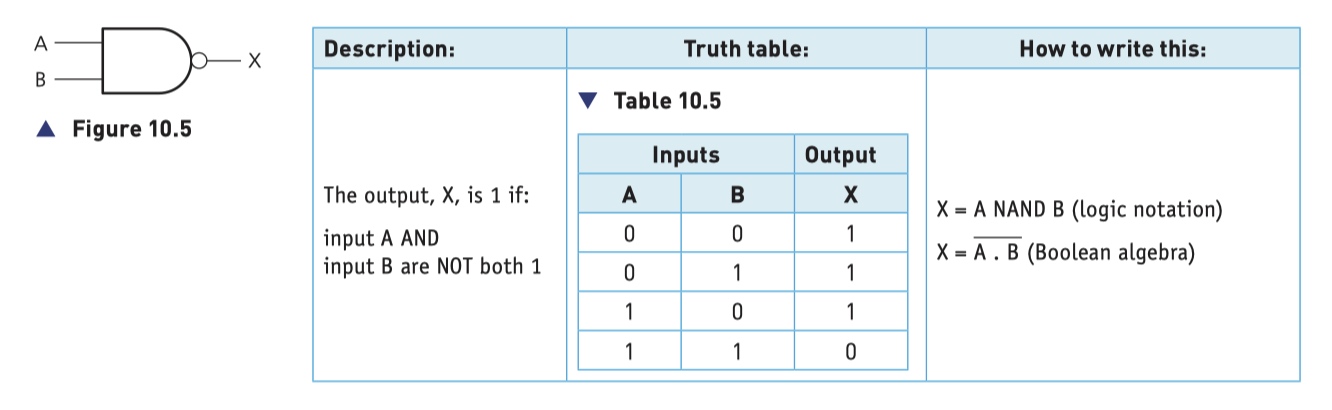
NAND Gate (NOT AND)
NOR Gate (NOT OR)

XOR Gate (XOR Gate)

- . represents the AND operation
- + represents the OR operation
- a bar (above the letter or letters, e.g. a) represents the NOT operation.
Example Constructing a truth table from a logic expression or logic circuit



Logic circuits, logic expressions, truth tables and problem statements
Type 1 - produce a truth table for a given logic circuit

题目:找出对应逻辑图(logic circuit)的真值表(truth table)
Step 1 - find the intermediate values P and Q

找出对应逻辑图(logic circuit)的真值表(truth table)

Step 2 - find intermediate values R use P and Q

找出对应逻辑图(logic circuit)的真值表(truth table)

Step 3 - find final part X use intermediate R and C

找出对应逻辑图(logic circuit)的真值表(truth table)

Final result

找出对应逻辑图(logic circuit)的真值表(truth table)

Type 2 - write logic expressions from given logic circuits
Example 1

- logic gate1::
(A AND B) - logic gate2::
(B OR C) - final result::
(A AND B) XOR (B OR C)
Example 2
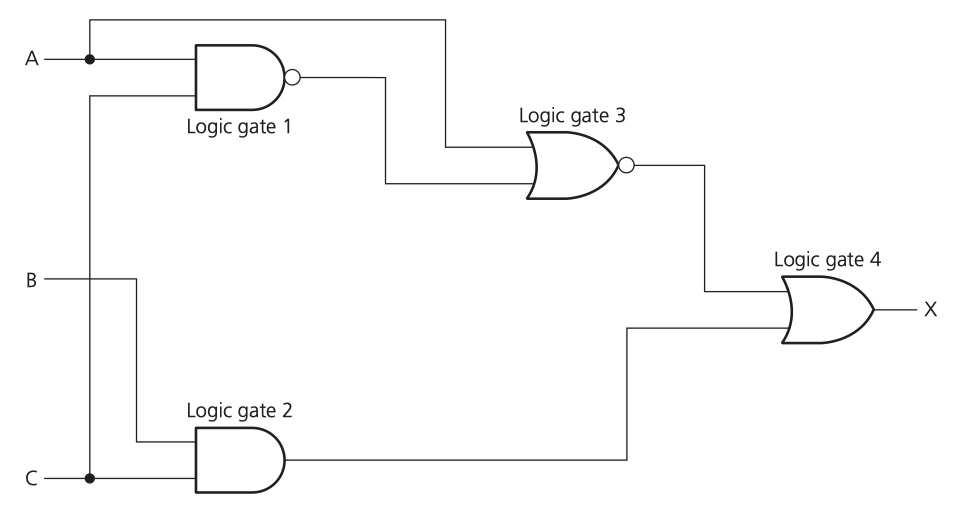
- logic gate 1::
(A NAND C) - logic gate 2::
(B AND C) - logic gate 3::
(logic gate 1) NOR A ~ ((A NAND C) NOR A) - logic gate 4::
((A NAND C) NOR A) OR (B AND C)
Type 3 - produce a logic circuit and a truth table from given logic expression
Example 1
Given logic expression: (A XOR C) OR (NOT C NAND B)
first step - A XOR C

second step - NOT C NAND B

third step - combine

fourth step - truth table

Type 4 - produce a logic expression and logic circuit from given truth table (optional)
Example 1

logic circuit

Example 2

logic circuit

Example 3

(NOT A AND NOT B AND NOT C)
(A AND NOT B AND NOT C)
(A AND B AND NOT C)
final logic expression
(NOT A AND NOT B AND NOT C)
OR (A AND NOT B AND NOT C)
OR (A AND B AND NOT C)