Chapter 1
Information Representation
Chapter 1 - Information Representation
- 1.01 Number Systems
- 1.02 Numbers and quantities
- 1.03 Internal coding of numbers
- 1.04 Internet coding text
- 1.05 Images
- 1.06 Sound
- 1.07 Data compression
1.01 Number Systems
二进制和十进制的来源
十进制的来源
人类计算使用十进制,可能是跟人类的手指有10根有关。数学来源于计数,最原始的方法就是数手指头。 亚里士多德称人类普遍使用十进制,只不过是绝大多数人生来就有10根手指这样一个解剖学事实的结果。
古罗马数字5进制
玛雅人的20进制
其他进制
二进制——最简单,但是使用起来较复杂
八进制——
十二进制——一年十二个月份,
十六进制——十六两合一斤
二十进制——玛雅人使用,手和脚一共有20根,来进行计数
二进制的来源
早期设计的机械计算装置中,使用的不是二进制,而是十进制或者其他进制,利用齿轮的不同位置表示不同的数值,这种计算装置可能更加接近人类的思想方式。比如说一个计算设备有十个齿轮,它们级连接起来,每一个齿轮有十格,小齿轮转一圈大齿轮走一格。这就是一个简单的十位十进制的数据表示设备了,可以表示0到999999999的数字。 配合其他的一些机械设备,这样一个简单的基于齿轮的装置就可以实现简单的十进制加减法了。
电子计算机出现以后,使用电子管来表示十种状态过于复杂,所以所有的电子计算机中只有两种基本的状态,开和关。
为什么要用二进制
- 电路中容易实现 :当计算机工作的时候,电路通电工作,于是每个输出端就有了电压。
- 用二进制表示数据具有抗干扰能力强,可靠性高等优点。因为每位数据只有高低两个状态,当受到一定程度的干扰时,仍能可靠地分辨出它是高还是低。
- 便于逻辑判断(是或非)。适合逻辑运算:逻辑代数是逻辑运算的理论依据,二进制只有两个数码,正好与逻辑代数中的“真”和“假”相吻合。
所有信息在计算机中都是二进制表达
The word 'Hello' is stored as the binary combination of 0100100001100101011011000110110001101111
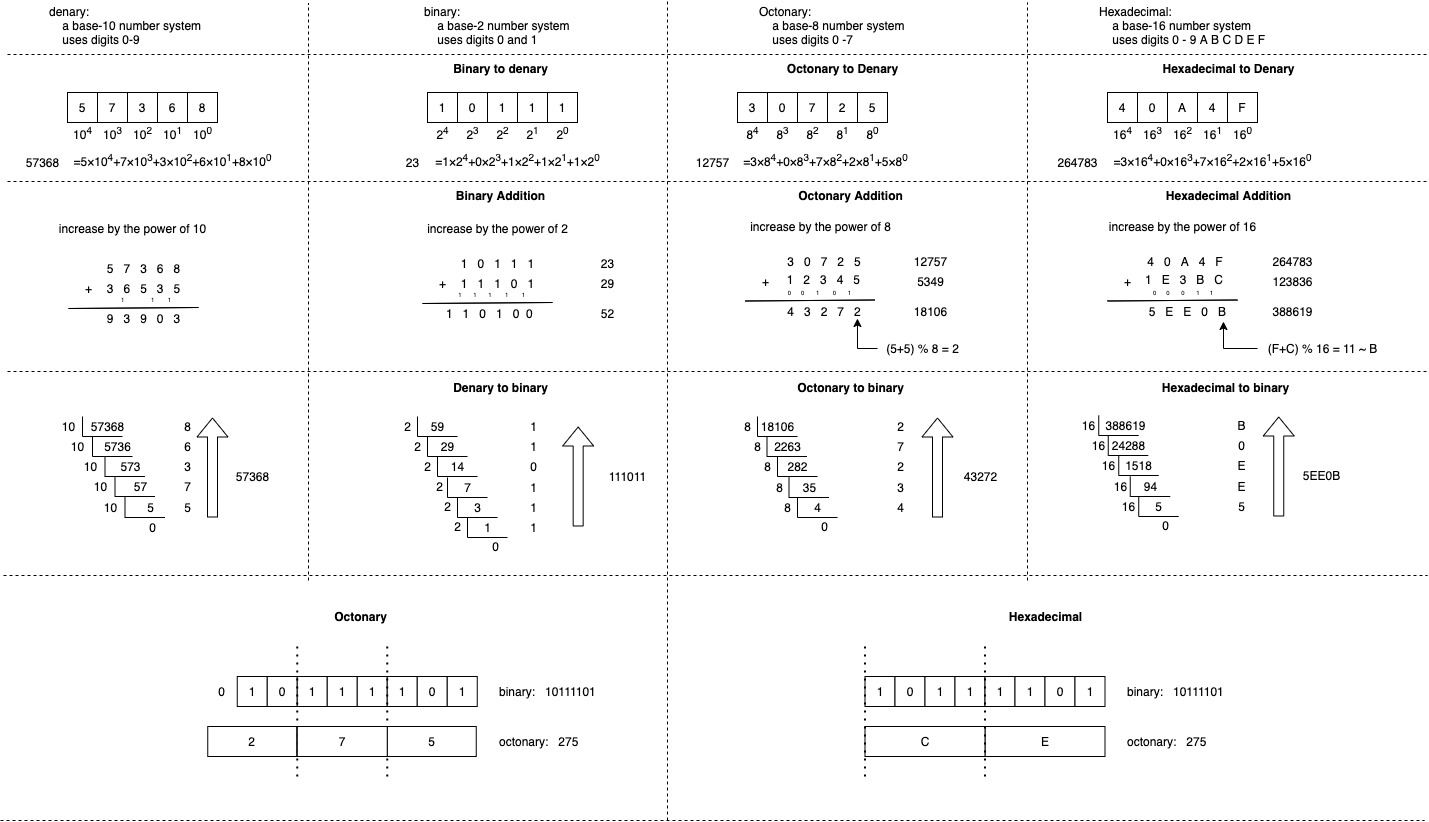
Denary, Binary, Octonary, Hexadecimal
Key Terms
- Denary numbers - which are also known as decimal numbers are written using one of the symbols 0,1,2,3,4,5,6,7,8,9 for each denary digit
- Bit - a digit in the binary number system written using either of the symbols 0 and 1
- Byte - a group of eight bits treated as a single unit
- Nibble - a group of four bits
Calculate
Overflow
Overflow:: a condition when the result of a calculation is too large to fit into the number of bits defined for storage
Hexadecimal number system examples
html color
html hexadecimal color (48 bits).
How many colors?

Mac Address
Media Access Control(MAC) address are 12-digit hexadecimal numbers that uniquely identify each different device in a network.
How many Mac Address?
00-1B-6384-45-E6
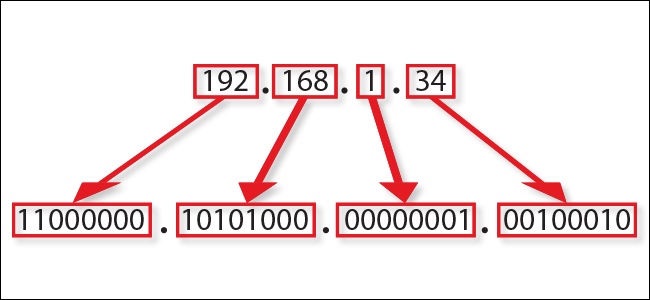
IP address
IP Address (32 bits).
How many Ip Address?
1.02 Numbers and quantities
Key Terms
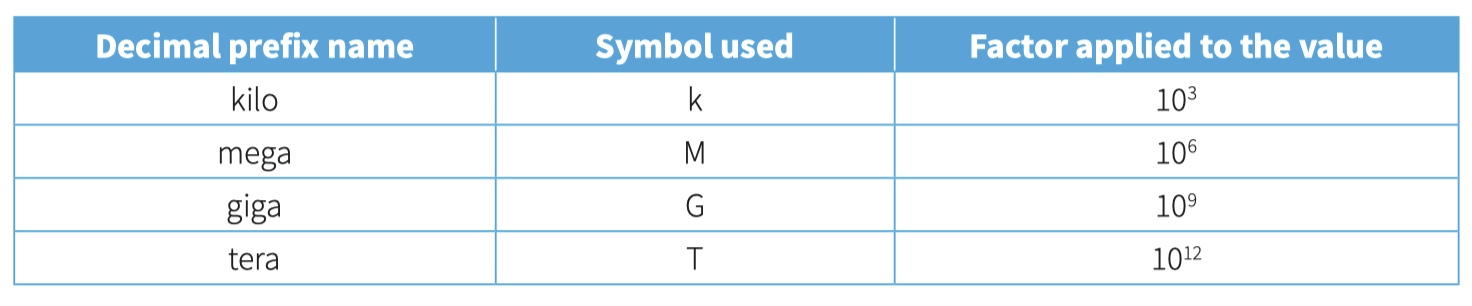
- Decimal prefix - A prefix to define the magnitude of a value. Examples are kilo, mega, giga and tera representing factors of 103 , 106 , 10 9 and 10 12 respectively.
- Binary prefix - A prefix to define the magnitude of a value. Examples are kibi, mebi, gibi and tebi representing factors of 210 , 220 , 2 30 and 2 40 respectively.
Type of numbers
- Integer, ex:: 3 or 47, A whole number used for counting
- Signed integer, ex:: −3 or 47, The positive number has an implied + sign
- Fraction, ex:: 2/3 or 52/17, Rarely used in computer science
- A number with a whole number part and a fractional number part, ex:: −37.85 or 2.83, The positive number has an implied + sign
- A number expressed in exponential notation, ex:: −3.6 × 10 8or 4.2 × 10–9, The value can be positive or negative and the exponent can be positive or negative
Prefix
decimal prefix
binary prefix
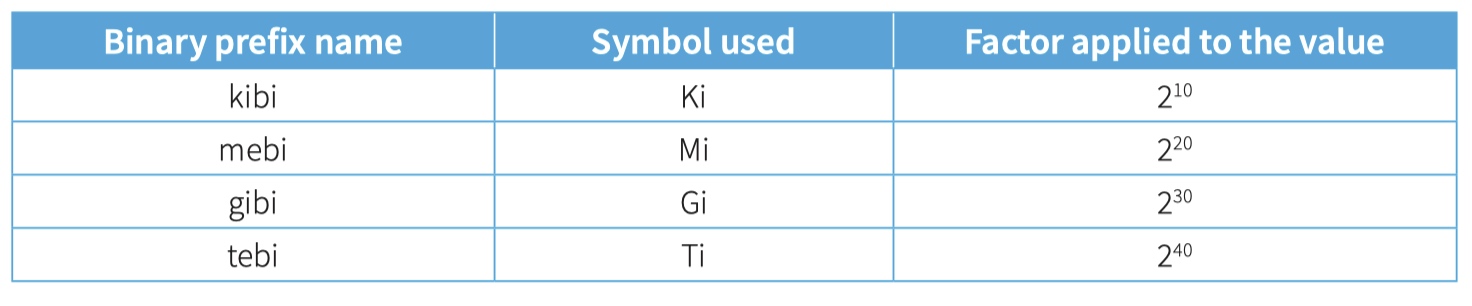
Image file prefix
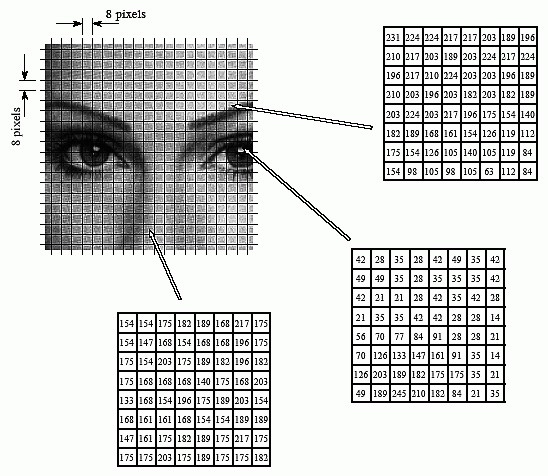
image with pixel 4160*3120::
R ~ 8 bits, G ~ 8 bits, B ~ 8 bits
RGB ~ 3 Byte
image file size:: 4160 * 3120 * 3 Byte = 38,937,600 Byte / 1024 = 38025 KiB /1024 = 37.13 MiB
1.03 Internal coding of numbers
Key Terms
- One’s complement - the binary number obtained by subtracting each digit in a binary number from 1
- Two’s complement - the one’s complement of a binary number, plus 1
- Overflow - a condition when the result of a calculation is too large to fit into the number of bits defined for storage
- Binary coded decimal (BCD) - storage of a binary value representing one denary digit in a nibble
- Packed BCD - when two BCD nibbles are stored in one byte
One's complement
对于小学生来说,会做5-3,但是不会做3-5。 后续我们就引入了负数的概念
3-5=3+[-5] = [-2] 中括号的数代表“反码“
计算机的数字电路只有加法器,没有减法器。既然可以用反码来做减法,所以不需要单独来设计减法器
3 = [0_0000011]
5 = [0_0000101] 符号位负数 -5 = [1_0000101] 反码 -5 = [1_11111010]
3 +[-5] =[-2]
[0_0000011]+[1_1111010]=[1_11111101]
为什么可以实现:
实际上反码可以理解为 -5 = [1_1111010] = 255 - 5
[3] + [-5] = 3 + 255 – 5 = 253 = 255 -2 = [-2]
[7] + [-5] = 7 + 255 – 5 = 255 + 2 = [2]
反码的问题:
[0_00000000] ~ +0 和 [1_11111111] ~ -0 所以存在两个0,这样在计算中是没有必要的
Two's complement
因为0 这个特殊的数字存在。0既不是正数也不是负数。
对于反码来说 正数 +0 ~ +127 负数 -127 ~ -0
所以会出现两个0
[0_0000000] +0
[1_1111111] -0
但是对于计算机来说任何数字都只能有一个编码。所以把负数整体向后移动一位,这样范围就变成 -128 ~ -1 0 ~ 127。 将这个反码+1 称为补码
补码:
正数的补码保持不变 3 = [0_0000011]
负数先求反码,然后再加1 -5 = [1_1111010] + 1 = [1_1111011]
3 +[-5] = [-2]
[0_0000011]+[1_1111011]=[11111110]
Binary coded decimal

This is useful in applications that require single denary digits to be stored or transmitted.
The BCD code uses a nibble to represent a denary digit.
1.04 Internet coding text
ASCII Code
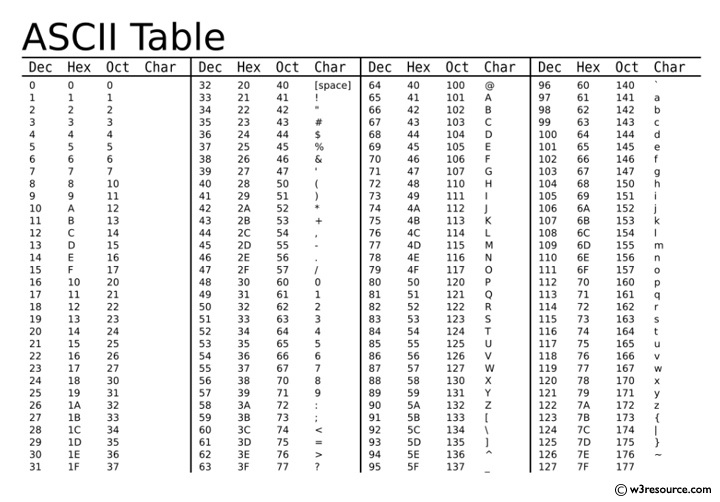
In AscII each character will take 1 byte of storage space as it is made up of 8 bits.
The 7-bit version of the code (often referred to as US ASCII) was standardised many years ago by ANSI (American National Standards Institute).
Unicode

In Unicode a character takes up 2 bytes as it is made up of 16 bits.
It should be noted that Unicode codes have been developed in tandem with the Universal Character Set (UCS) scheme, standardised as ISO/IEC 10646
Note that for the two-byte, three-byte and four-byte representations all continuing bytes have the two most significant bits set to 10.
编码集推荐阅读 -> 从ASCII码->Unicode->UTF-8历史变迁,及其差异
1.05 Images
Key Terms
- Vector graphic - a graphic consisting of drawing objects defined in a drawing list
- Drawing object - a component defined by geometric formulae and associated properties
- Drawing list - contains one set of values for each drawing object
- Property - defines one aspect of the appearance of the drawing object
- Picture element (pixel) - the smallest identifiable component of a bitmap image, defined by just two properties:: its position in the bitmap matrix and its colour
- Colour depth - the number of bits used to represent one pixel
- Bit depth - the number of bits used to represent each of the red, green and blue colours
- Image resolution - the number of pixels in the bitmap file defined as the product of the width and the height values
- Screen resolution - the product of width and height values for the number of pixels that the screen can display
- File header - a set of bytes at the beginning of a bitmap file which identifies the file and contains information about the coding used
Vector graphics

- drawing list
- drawing object
- property
Bitmap
Image represented by a binary value. "bit-plane". 1-bit would give us 2 colors, 2-bits would give us 4 colors, 3-bits would give us 8 colors.
1-bit picture 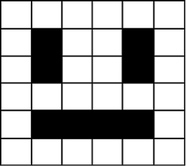
1-bit picture 
2-bits 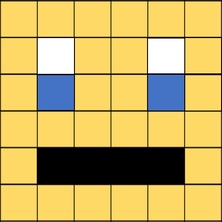
2-bits 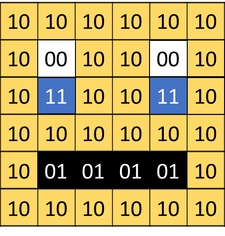
2-bits 
- Color depth – how many bits represent each pixel
- Resolution - Width & Height (in pixels)
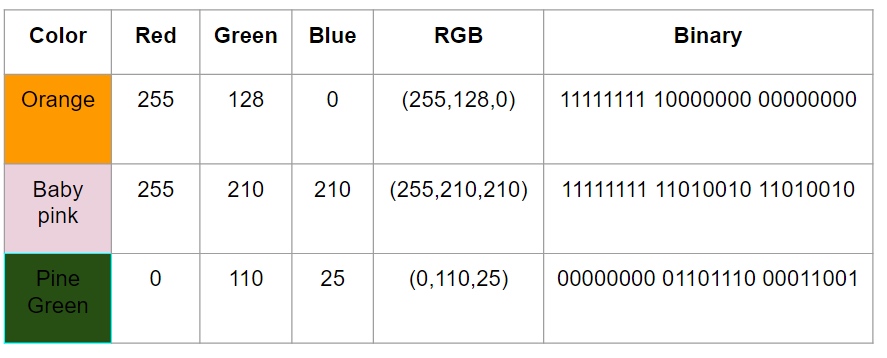
RGB color
color depth 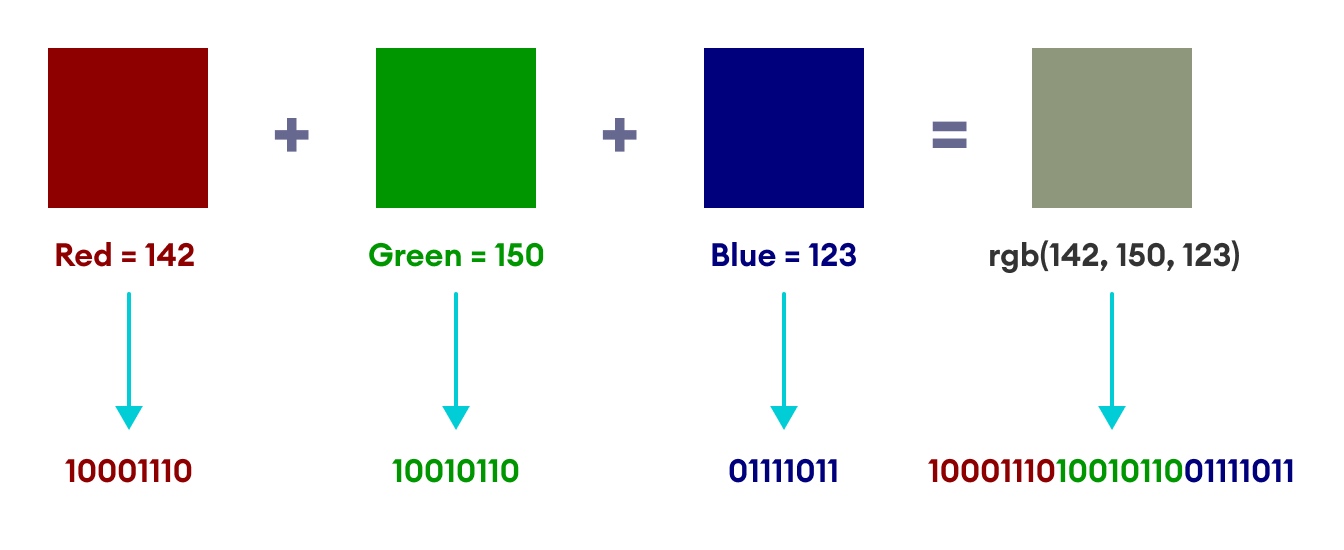
color meaning
gray graphics
Compare Overall Findings
Vector
- Made of shapes.
- More scalable without losing quality.
- More specialized uses.
Bitmap
- Made of pixels.
- Compatible with Microsoft Paint, Adobe Photoshop, Corel Photo-Paint, Corel Paint Shop Pro, and GIMP.
- Lose quality when the image is resized larger.
Format compare
vector
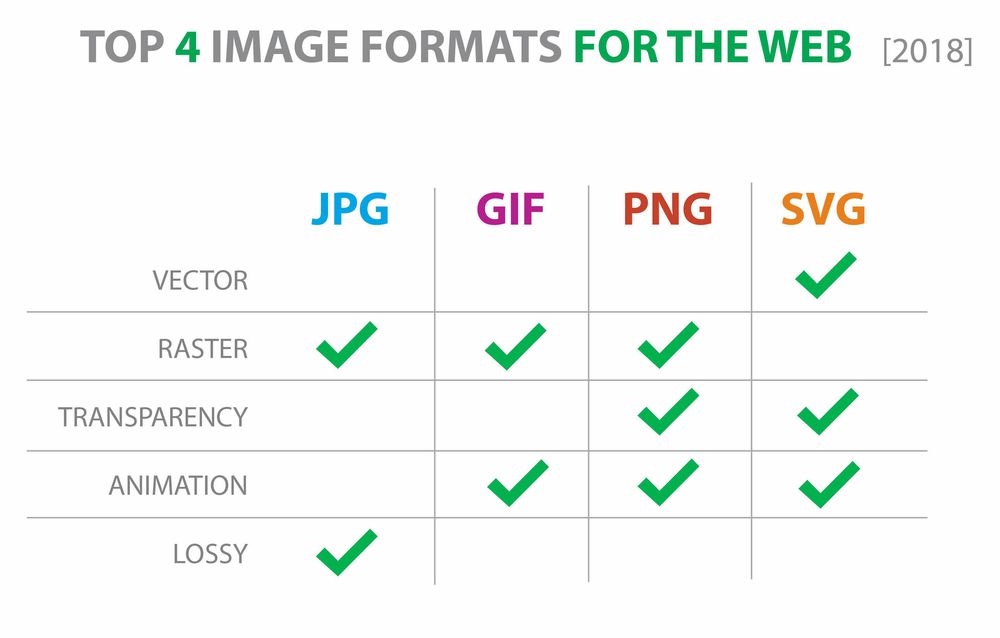
Includes AI, CDR, CMX (Corel Metafile Exchange Image), SVG, CGM (Computer Graphics Metafile), DXF, and WMF (Windows Metafile).
Bitmap
Includes GIF, JPG, PNG, TIFF, and PSD.
Easy of use - Vectors Are More Robust
vector
- Resolution-independent.
- Maximum quality regardless of scale.
Bitmap
- Lose quality when scaling.
- Easier to go from vector to bitmap than the other way.
File header
A bitmap file has to store the pixel data that defines the graphic, but the file must also have a file header that contains information on how the graphic has been constructed.Because of this, the bitmap file size is larger than the size of the graphic alone. At the very least the header will define the colour depth or bit depth and the resolution.
- A vector graphic is chosen if a diagram is needed to be constructed for part of an architectural, engineering or manufacturing design.
- If a vector graphic file has been created but there is a need to print a copy using a laser or inkjet printer the file has first to be converted to a bitmap.
- A digital camera automatically produces a bitmap.
- A bitmap file is the choice for insertion of an image into a document, publication or web page.
1.06 Sound
Key Terms
- Analogue data - data obtained by measurement of a physical property which can have any value from a continuous range of values
- Digital data - data that has been stored as a binary value which can have one of a discrete range of values
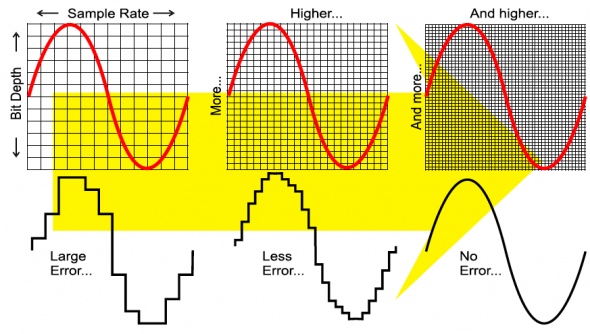
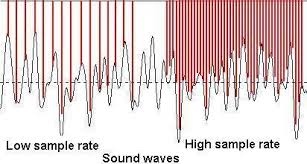
- Sampling - taking measurements at regular intervals and storing the value
- Sampling resolution - the number of bits used to store each sample
- Sampling rate - the number of samples taken per second
Analogue Devices
All analogue devices use analogue data. Examples of analogue devices include::
- Microphone
- Headphones
- Loud Speaker
- Sensors (temperature, pressure etc)
Digital Devices

All digital devices use digital data. Examples of digital devices include::
- Computers/Laptops/IPads
- Mobile Phone
- MP3 Player
- Digital Camera
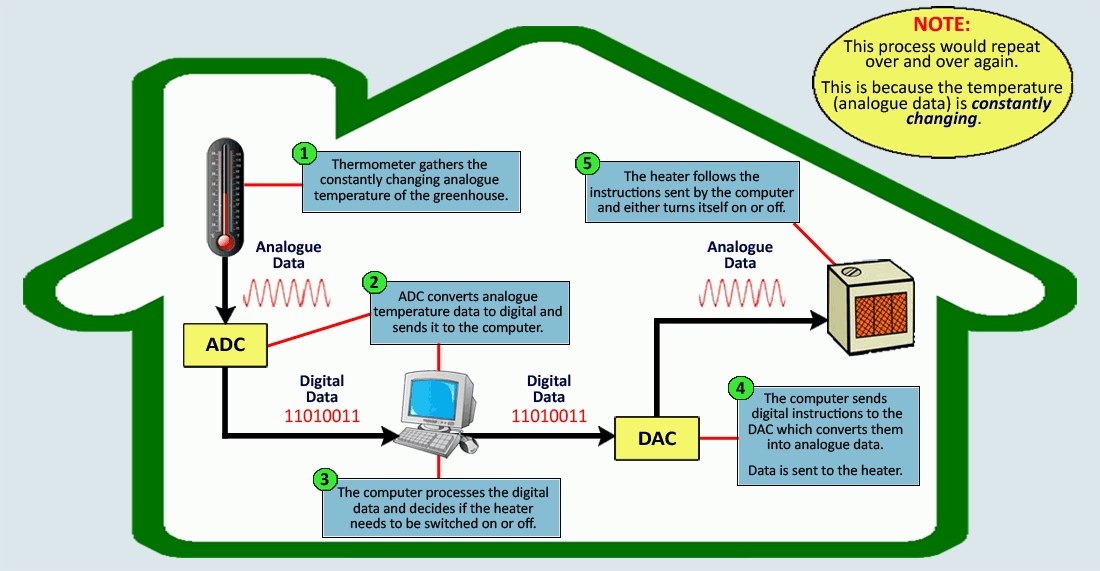
Analogue to Digital Converter (ADC)
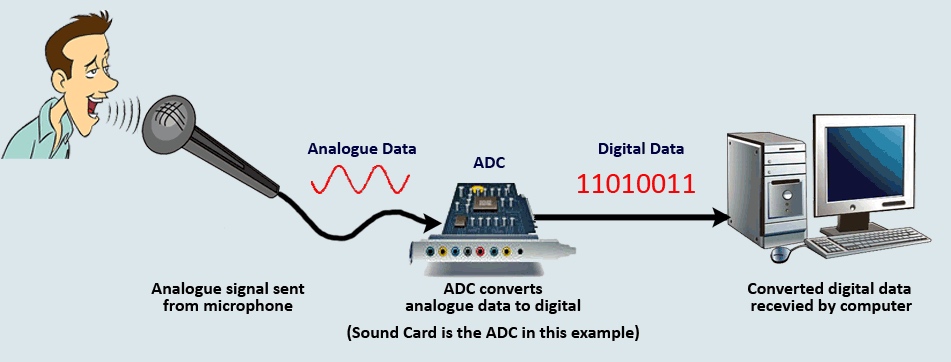
- If we try to attach an analogue device (like a microphone) to a computer we will need to convert the analogue data to digital before the computer can use it.
- The microphone is used to pass the analogue sound waves through the ADC which will convert the sound from analogue to digital.
- The ADC then passes the converted digital data into the computer where the sound can be stored and edited.
Digital to Analogue Converter (DAC)
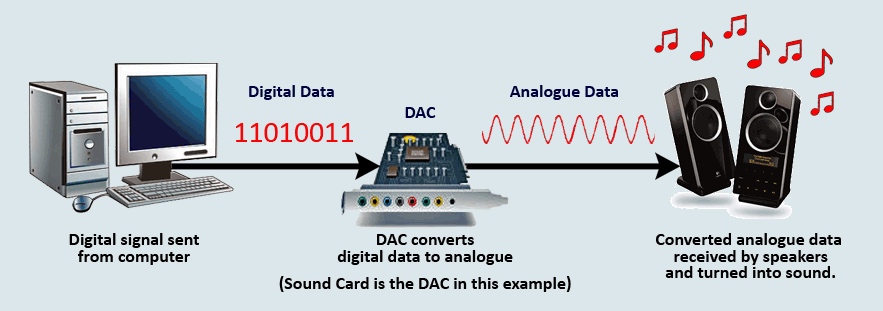
- If we want to listen to digital music (like mp3's) we would need to attach an analogue device such as loud speakers or headphones to our computer.
- The computer will pass the digital sound values through a DAC (located on a sound card) which will convert the digital data to analogue.
- The DAC then passes the converted anologue data onto the analogue loud speaker which we would then hear as sound waves.
IOT
Sound
sampling
sampling
The sound we hear is also analogue.computers work digitally and can only process binary.
Sound is recorded at set timed intervals; this process is known as sampling.
1.07 Data compression
Key Terms
- Lossless compression:: coding techniques that allow subsequent decoding to recreate exactly the original file
- Lossy compression:: coding techniques that cause some information to be lost so that the exact original file cannot be recovered in subsequent decoding
Huffman coding

Instead of having each character coded in one byte, the text is analysed to find the most often used characters. These are then given shorter codes. The original stream of bytes becomes a bit stream.
vector graphic file compression
If a vector graphic file needs to be compressed it is best converted to a Scalable Vector Graphics format. This uses a markup language description of the image which is suitable for lossless compression.
Image and sound compression
Lossy compression can be used in circumstances where a sound file or an image file can have some of the detailed coding removed or modified. This can happen when it is likely that the human ear or eye will hardly notice any difference.
For a bitmap a simple lossy compression technique is to establish a coding scheme with reduced colour depth. Then for each pixel in the original bitmap the code is changed to the one in the new scheme which represents the closest colour.
Image formats